Michaelmas Term Part IB Computing Course - Programming in Octave or Matlab
by Paul Smith, Peter Long, Richard Prager and S.S. Singh
In addition to this document you will need the Introduction to Octave by Peter Long and Paul Smith. This lab involves reading the tutorial material in the "Introduction to Octave" and then completing the exercises in this handout.
This course provides an introduction to computing using Octave. It will teach you how to use Octave to perform calculations, plot graphs, and write simple computer programs to calculate numerical solutions to mathematical problems.
There are four exercises, one for each of your four lab sessions. Each exercise must be marked up by the end of the appropriate lab session.
The lecturer in charge of this course is Prof Byrne.
Student: College: Group:
Exercise 1: Date: Marker: Exercise 2: Date: Marker: Exercise 3: Date: Marker: Exercise 4: Date: Marker:
Please contact Prof Byrne (wjb31) with any queries.
Exercises and Marking
There are four exercises. One exercise should be completed and marked up in each of the lab sessions. The first exercise must be marked up by the end of the first lab session, the second exercise must be marked up by the end of the second lab session, and so on. There will be no marks for late submissions. The table below summarises the exercises, their marks and timing. The qualifying mark for standard credit is 12.
| Exercise | To be marked by | Marks | |
| 1 | πe vs eπ | end of first session | 3 |
| 2 | Finding π using the arctangent series | end of second session | 3 |
| 3 | The Newton-Raphson method | end of third session | 3 |
| 4 | Euler angles | end of fourth session | 3 |
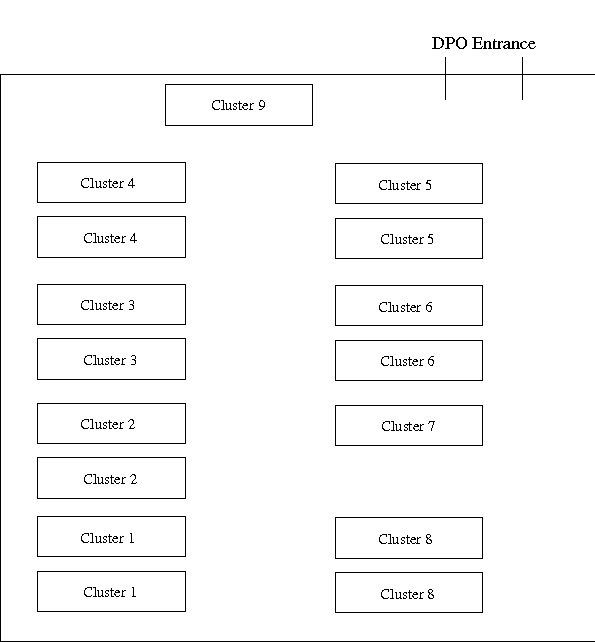
Cluster allocation and attendance
You have been assigned a particular DPO cluster to work at. Use the table on the next page to find your cluster. Each cluster is supervised by a particular demonstrator. To avoid being marked late, you must have signed in with your demonstrator by the start of each session.
All sessions start at five minutes past the hour and finish at five minutes to the hour. The first session begins with a short talk, but at the start of all subsequent sessions students should go straight to the DPO.
All lab sessions are compulsory and may not be missed without penalty unless you have completely finished all the exercises in this handout. Students arriving up to 10 minutes late (by 15 minutes past the hour) will lose 1 mark. Students arriving more than 10 minutes late (i.e. after 15 minutes past the hour), will lose 2 marks. A student who leaves a lab session, and then returns, may be penalised as if they had arrived more than 10 minutes late.
If you miss, or are late for a lab session because of illness or other grave cause, you should first contact Prof Byrne to try and arrange a time to catch up the work missed. You will need to submit the standard Allowances for Illness form to the Teaching Office to apply for remission of any penalty imposed, or for an allowance of marks if it proves impossible to re-arrange the session. Contact Prof Byrne with any problems or queries.
Getting started
Log in to your terminal and create a new folder to keep your work in. Call your folder 1boctave. This can be done by clicking the terminal icon that appears on the taskbar (or panel). A command window now opens and type the following:
wjb31@tw405:~> mkdir 1boctave
wjb31@tw405:~> cd 1boctave
Alternatively, you should see an icon for your home folder on the screen. Double click it and the folder opens. Now right click the mouse button in the space where all the folders appear and a menu pops up. Select menu item Create Folder.
Start up Octave by clicking Applications in the taskbar: All CUED Applications -> 2nd Year -> Start 1BOctave. When the Octave command window appears, move into your 1boctave folder using the following command and commence your lab:
octave:1> cd 1boctave
Cluster allocation as a function of lab group number
| Session | Lab groups | DPO Cluster |
| Monday, weeks 1-4 | 19-26 | 1 |
| Monday, weeks 1-4 | 27-34 | 2 |
| Monday, weeks 1-4 | 35-42 | 3 |
| Monday, weeks 1-4 | 97-104 | 4 |
| Monday, weeks 1-4 | 105-112 | 5 |
| Monday, weeks 1-4 | 113-114 | 9 |
| Tuesday, weeks 1-4 | 1-8 | 1 |
| Tuesday, weeks 1-4 | 9-16 | 2 |
| Tuesday, weeks 1-4 | 17,18,79-84 | 3 |
| Tuesday, weeks 1-4 | 85-92 | 4 |
| Tuesday, weeks 1-4 | 93-96 | 5 |
| Monday, weeks 5-8 | 61-68 | 1 |
| Monday, weeks 5-8 | 69-76 | 2 |
| Monday, weeks 5-8 | 77,78,133-138 | 3 |
| Monday, weeks 5-8 | 139-146 | 4 |
| Monday, weeks 5-8 | 147-154 | 5 |
| Monday, weeks 5-8 | 155-156 | 9 |
| Tuesday, weeks 5-8 | 43-50 | 1 |
| Tuesday, weeks 5-8 | 51-58 | 2 |
| Tuesday, weeks 5-8 | 59,60,115-120 | 3 |
| Tuesday, weeks 5-8 | 121-128 | 4 |
| Tuesday, weeks 5-8 | 129-132 | 5 |
Part IB Computing Course - Session 1
Read through sections 1. Introduction to 5. Plotting graphs of the tutorial guide and work through the examples. You should now be able to:
- Perform simple calculations by typing expressions in at the Octave prompt
- Assign values to variables and use these in expressions
- Build vectors and use them in calculations
- Plot 2D graphs
Now do exercise 1 and get it marked as described below by the end of the lab session.
Exercise 1: πe vs eπ
A. Exercise
- Which is larger, πe or eπ? Use Octave to evaluate both expressions.
- We shall now consider the general cases of xe and ex. Use Octave to plot graphs of these two functions, on the same axes, between the values of 0 and 5. Display the two graphs using different line colours and label them fully. You will need to keep this figure on the screen to show your demonstrator.
- In a separate figure, plot and label the graph of y=xe - ex, again between x-values of 0 and 5. For what value of x does xe=ex?
B. Implementation notes
- Tutorial sections - The tutorial sections immediately preceding this exercise give a number of examples of plotting graphs and performing calculations. Make sure that you have read these sections fully before you start this exercise.
- Octave constants and functions - Both π and e are known to Octave. The variable pi holds the value of π, and the function exp(x) returns the value of ex. Remember that e1 = e.
- Powers of scalars and vectors - To raise a single number (a scalar) to a power, you use the ^ operator. If you want to raise each element of a vector to a power, you must use the .^ operator, with the dot to say 'this is a element-by-element operation'.
- Preparing graphs - To make a start with your graphs, define the vector of numbers for your x-axis. You can use either the linspace function, or the colon notation. Once you have this vector, use it in your arithmetic to create a new vector(s) containing the y values.
C. Evaluation and marking [3 marks]
Show your two figures to a demonstrator for marking. Tell the demonstrator which of πe or eπ is larger, and at what value the functions xe or ex are equal.
Part IB Computing Course - Session 2
Read through sections 6. Octave programming I and 7. Control statements of the tutorial guide and work through the examples. You should now be able to:
- Create and use scripts to store a series of commands
- Use loops and conditionals to control program execution
Now do exercise 2 and get it marked as described below by the end of the lab session.
Exercise 2: Finding π using the arctangent series
A. Theory
The search to determine π to a greater and greater accuracy has occupied mathematicians for millennia. Euler and Archimedes had both devised methods for calculating π. Archimedes' approach, of inscribing and circumscribing circles, was the method of choice from the 3rd century BC until the 17th century AD. In 1671, James Gregory (1638-1675) found the now-standard power series for arctangent, which can be found in the Mathematics Databook:
tan-1 z = z - z3/3 + z5/5 - ...
Three years later, Gottfried Wilhelm Leibniz (1646-1716) independently found and published the same series, noting a special case: that tan π/4 = 1. In other words, putting z = 1 into the arctangent series, gives an approximation for π/4, and hence for π. The arctangent series is still the way that π is calculated today.
In 1699, Abraham Sharp (1651-1742) broke the previous record for the accuracy of π, finding 72 digits (which may not seem many, but is more than the native accuracy of Octave). He also used the arctangent series but realised that if, instead of z=1, he used the identity tan π/6 = 1/sqrt(3), he would get much quicker convergence.
We will try both these approaches.
B. Exercise
- Write a Octave script to calculate the first 50 terms in the arctangent series using z=1 and plot a graph showing the value of π estimated after each term. Calculate the difference between your estimate and π after 25, 30 and 50 terms.
- Now modify the script to also calculate the first 50 terms in the estimate for π using z=1/sqrt(3), plotting these in a different colour on the same graph. Why do you think the second series converges so much faster? Again, calculate the difference between your estimate and π after 25, 30 and 50 terms. What behaviour do you see, and why?
- The usual solution to this exercise is to use a for loop to step through the series, calculating the term and adding it on. However, the solution can instead be vectorised, i.e. performed entirely using vector calculations. This runs much faster (because Octave is good at vectors), and can be written in just one line. Try writing the general equation for the nth term of the series in such a way that it will also work when a vector is given to it. Give it a vector of numbers from 1 to 50, pass the result through the cumsum (look it up in the help system) function and finally plot that vector to give the answer. Try this approach, and the solution with a for loop, with 50,000 terms to see the difference that vectorising makes. Be prepared to wait a while for the for loop solution!
C. Implementation notes
- Try things out in Octave first - Remember that a Octave script is just a series of commands that you could equally well type in at the command line. Try things out in Octave first of all, before adding them to the script.
- Read error messages from bottom to top - If you get errors when you run your script, remember that these are best read from bottom to top.
- Alternating signs and odd numbers - You can get a sequence of alternating signs by using (-1)n, which is +1 when n is even, and -1 when n is odd. To produce only odd numbers from a counting sequence involving all positive integers n, you can use (2n - 1).
- Don't plot points inside the loop - Producing output to the screen or a file is the slowest part of many programs, and you should think about how to keep I/O to a minimum if you want to write an efficient program. If you plot each point as you calculate it inside your loop, the program will run very slowly. Instead, store your points in a vector as you calculate them and then output them all in one go at the end of the script. This will also allow you to join the points up, and to easily extract the spot points that the exercise asks for.
D. Evaluation and marking [3 marks]
Save the Octave commands necessary to create and plot the two functions in a script. Show this working script, and the plot, to a demonstrator for marking. Explain why the z=1/sqrt(3) series converges faster, and why it behaves as it does for a high number of terms.
Part IB Computing Course - Session 3
Read through section 8. Octave programming II of the tutorial guide and work through the examples. You should now be able to:
- Define and use your own functions
Exercise 3: Finding roots by the Newton-Raphson method
A. Theory
You may have come across the Bisection method for finding the solution to f(x)=0. The Bisection method, which simply finds points where the function changes sign, is a perfectly acceptable method, but can converge rather slowly. A better approach is to use extra information: the derivative of the function as well as its value, and this is the basis of Newton's method, commonly called the Newton-Raphson method.
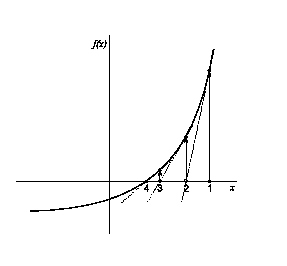
Example of the Newton-Raphson method. Starting from an initial guess (labeled '1'), the local derivative is extrapolated to generate the next guess of the root, and so on.
The method is best understood graphically, as demonstrated in the Figure. The tangent line to the curve is calculated at the current guess, xi, (here starting at point '1') and is extrapolated until it crosses the x-axis. This x-value is then the next guess, xi+1, and the process is repeated.
Algebraically, Newton-Raphson derives from the Taylor series, with which you should already be familiar from the IA Mathematics course. This states how the value of the function at a new (nearby) point x+h can be calculated from the value and derivatives at a known point x:
f(x+h) = f(x) + hf'(x) + h2/2! * f''(x) + ...
To find a root of our function, let us say that our current guess is at x and we want to find out how much to move to get to the root. Calling this correction term h, this means that the root is at x+h and so, by definition, f(x+h)=0. Using the Taylor series expansion:
f(x+h) = f(x) + hf'(x) + h2/2! * f''(x) + ... = 0
If h is small and the function is well-behaved then we can neglect the higher-order terms and just use a linear approximation, needing only the first derivative:
f(x) + hf'(x) (approx)≈ 0
and so the correction term h can be estimated by
h (approx)≈ -f(x)/f'(x)
The update rule for Newton-Raphson just applies this correction at each iteration, i.e.
Given an initial guess, x0, we iterate according to the equation) until the desired accuracy is reached. Being a numerical solution, and given the limits to floating-point accuracy, it may not be possible to exactly reach the root. Instead, it is usual to continue until the difference between successive estimates is below a certain tolerance (i.e. we are close enough for our purposes).
The Newton-Raphson method is very powerful, and it is the method of choice for any function whose derivative can be evaluated efficiently, and is continuous and non-zero in the neighbourhood of the root. It is also not restricted to just one-dimensional problems, and readily generalises to multiple dimensions. Its main power lies in its rate of convergence: near the root it converges quadratically, meaning that the number of significant digits approximately doubles with each step. However, it is important to start near the neighbourhood of the root and to be sure the function is well-behaved there, so plotting the graph of the function whose root you are finding is a very useful first step.
B. Exercise
We shall use the Newton-Raphson method to find the roots of
f(x) = x^5 - 5x^4 + x^2 - 8x + 50
to a tolerance of 0.00001.
- Write two functions: fun(x), which returns the value of f(x) (see the equation) for a given value of x; and dfun(x), which returns the value of its derivative, f'(x). Plot both of these over the range -3 to 6. Check that they appear correct, and make initial guesses to the values of the roots (to the nearest whole number will do).
- Write a third function, newton(x, tol) which performs the Newton-Raphson estimation of a root. This should make use of fun and dfun, iterate according to the equation and return the final estimate. The first parameter, x, is the initial guess x0. The second parameter, tol is the tolerance; the iteration stops once the difference between successive estimates is less than this.
- Find all of the real roots of the equation to the specified tolerance. Which root do you find with an initial guess of 0, and why is this not one of the nearby roots? Are there any cases where the Newton-Raphson method will fail to find a root?
- The newton function you have just written is not as general as it could be, since it assumes that the functions called fun and dfun exist, and do what they are supposed to do. This can be improved by passing the names of the functions to newton as two additional parameters. These function names are passed as strings, and you can tell Octave to run a function named by a string using the feval command: feval(fname, parameters, ...) where fname is the function name string, and parameters, ... are the parameters to pass to it. Modify your newton function to use feval rather than referring to fun and dfun.
C. Implementation notes
- Writing functions - Don't forget that each of your three functions needs to be in a separate M-file, each with the same name as the function except for the .m added. Each file should begin with a function line, and then some help comments.
- Loops - Think carefully about what kind of loop you need in newton.m to perform the iteration, and what the termination criterion is.
- Absolute errors - Remember, when you check whether the remaining error is less than tol, that the error value could be negative. Use the abs function to take the absolute value of this error.
D. Evaluation and marking [3 marks]
Show your graphs to your demonstrator, and your various M-files. Run your newton function to show it finding a root, and explain what happens in any unusual cases.
Part IB Computing Course - Session 4
Read through sections 9. Matrices and vectors and 10. Basic matrix functions of the tutorial guide and work through the examples. You should be able to:
- Define matrices in Octave
- Use matrices and vectors in simple calculations
- Perform standard operations on matrices
Now do exercise 4 and get it marked as described below by the end of the lab session.
Exercise 4: Euler angles
A. Theory
A rotation matrix in two dimensions is easy to define. There is only one axis of rotation, which is normal to the 2D plane, and a rotation of a positive angle θ (in a right-handed co-ordinate system) is given by the matrix
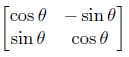
Defining rotations in three dimensions is more difficult. One method of defining rotations is known as Euler angles, which are often used in mechanics. (Leonhard Euler (1707-1783) had also proposed a method for finding π.)
The method of Euler angles, specifies three angles. These are commonly called azimuth, elevation and roll (or in aeronautical terms yaw, pitch and roll). We shall label these three angles as α, η and ρ, and our object exists in a normal right-handed co-ordinate set, z, y and x.
The rotations must be applied in a specific order. A point (x, y, z) is first rotated from its original location by an angle ρ about the x axis (roll):
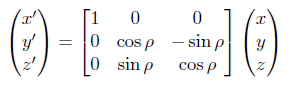
Then it is rotated by an angle η about the original y axis (elevation):
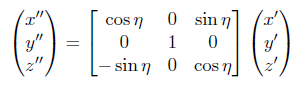
The final rotation, α is then about the original z axis (azimuth), defining the new location x''', y''' and z''' as
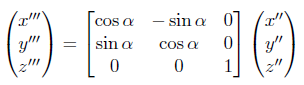
These three equations can be combined to give the following overall result.
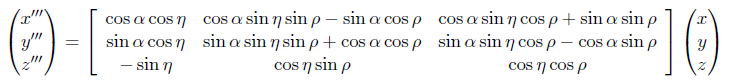
B. Exercise
- Write a Octave function which takes as parameters three Euler angles and returns a single 3D rotation matrix, transforming points (x, y, z) to (x''', y''', z'''), as defined above. It is best to do this by creating three simple rotation matrices and multiplying them together to get the required result, rather than using the complicated overall equation.
- Now write a separate script, in which you call the function written in part 1 in order to find the rotation matrix R which rotates a co-ordinate system by the Euler angles 90o, 20o, 15o. After calling this function, your script should verify that the matrix returned is a valid rotation matrix i.e. that it is orthogonal, and has a determinant of +1.
- The point p = (2,3,0)T is to be mapped to a new location q using the matrix R from part 2. Add commands to your script to define p and find q. Which matrix reverses this transformation?
- Extend your script to also find the matrix S which represents the rotation given by -90o, -20o, -15o. Transform the vector q, found in part 3, using the matrix S to give a new vector r. Why does r not equal p?
- Write a function to calculate the three Euler angles that describe the transformation represented by a 3 * 3 orthogonal rotation matrix. Your function should take a matrix as its argument and return a vector of the three angles The azimuth α and roll ρ should be in the range -180 to +180 degrees. The elevation η should be in the range -90 to +90 degrees.
- Use the function you wrote in part (5) above to find the Euler angle description of the transformation that maps q back to p.
D. Implementation notes
- Degrees and radians - Remember that Octave works in radians, not degrees. You might like to make use of the sind function you defined earlier, and also to define a cosd function.
E. Evaluation and marking [3 marks]
Show your two M-files (the Euler angle function and the main script) to a demonstrator, and run them to show the calculations. Explain why the matrices behave as they do.