LATEX maths and graphics
Tim Love
May 11, 2012
Copyright © 2004-2012 by T.P. Love. This document may be copied freely for the purposes of education and non-commercial research. Cambridge University Engineering Department, Cambridge CB2 1PZ, England.This handout assumes that you have already read the Advanced LaTeX document. Note that there's an alternative way of producing maths in LATEX - AMS-LATEX. See the for details. If you want to more more about graphics, see by Keith Reckdahl. Comments and bug reports to Tim Love (tl136).
Contents
1 Maths1.1 Environments
1.2 Special Characters
1.2.1 Greek
1.2.2 Miscellaneous
1.2.3 Arrows
1.2.4 Calligraphic
1.2.5 Character Modifiers
1.2.6 Common functions
1.3 Subscripts and superscripts
1.4 Overlining, underlining and bold characters
1.5 Roots and Fractions
1.6 Delimiters
1.7 Numbering and labelling
1.8 Matrices
1.9 Macros
1.10 Packages
1.11 Fine tuning
1.12 Maths and Postscript fonts
1.13 Matlab and LaTeX
1.14 Examples
2 Graphics
2.0.1 psfrag: adding maths to postscript files
2.1 Scaling, rotation, clipping, wrap-around and shadows
1 Maths
There's more to maths typesetting than meets the eye. Many conventions used in the typesetting of plain text are inappropriate to maths. LATEX goes a long way to help you along with the style. For example, in a LATEX maths environment, letters come out in italics, `-' as `−' (minus) instead of the usual `-' (dash), `*' becomes *, ' becomes ′ and spacing is changed (less around `/', more around `+'). Many of the usual LATEX constructions can still be used in maths environments but their effect may be slightly different; eg \textbf{ } only affects letters and numbers. `{' and `}' are still special characters; they're used to group characters. As usual in LATEX you can override the defaults, but think before doing it: maths support in LATEX has been carefully thought out and is quite logical though the LATEX source text may not be very readable. It's a good idea to write out the formulae on paper before you start LATEXing, and try not to overdo the use of the `\frac' construction; use `/' instead.1.1 Environments
There are 2 environments to display one-line equations.- equation:-
- Equations in this environment are numbered.
\begin{equation} x + iy \end{equation}x + iy (1) - displaymath:-
- These won't be numbered. \[, \]
can be used as abbreviations for \begin{displaymath} and
\end{displaymath}.
\begin{displaymath} x + iy \end{displaymath}x + iy
- math:-
- For use in text. \( and \) can be used to delimit the environment, as can the TEX constructions $ and $ . For example, $x=y^2$ gives x=y2.
- eqnarray:-
-
This is like a 3 column tabular environment. Each line by default is numbered.
You can use the eqnarray* variant to suppress numbering altogether.
\begin{eqnarray} a1 & = & b1 + c1\nonumber\\ a2 & = & b2 - c2 \end{eqnarray}a1 = b1 + c1 a2 = b2 − c2 (2)
1.2 Special Characters
The The Comprehensive LATEX Symbol List document offers 105 pages of symbols. Here are just a few.1.2.1 Greek
| α | \alpha | β | \beta | γ | \gamma | δ | \delta | ϵ | \epsilon |
| ζ | \zeta | η | \eta | θ | \theta | ι | \iota | κ | \kappa |
| λ | \lambda | μ | \mu | ν | \nu | ξ | \xi | o | o |
| π | \pi | ρ | \rho | σ | \sigma | τ | \tau | υ | \upsilon |
| ϕ | \phi | χ | \chi | ψ | \psi | ω | \omega | Γ | \Gamma |
| ∆ | \Delta | Θ | \Theta | Λ | \Lambda | Ξ | \Xi | Π | \Pi |
| Σ | \Sigma | Υ | \Upsilon | Φ | \Phi | Ψ | \Psi | Ω | \Omega |
1.2.2 Miscellaneous
| … | \ldots | … | \cdots | : | \vdots |
| ··· | \ddots | ± | \pm | ± | \mp |
| × | \times | ÷ | \div | ∗ | \ast |
| ∗ | \star | ° | \circ | • | \bullet |
| · | \cdot | ∩ | \cap | ∩ | \bigcap |
| ∪ | \cup | ∪ | \bigcup | 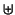 | \uplus |
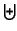 | \biguplus | 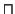 | \sqcap | 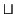 | \sqcup |
 | \bigsqcup | ∨ | \vee | ∨ | \bigvee |
| ∧ | \wedge | ∧ | \bigwedge | \ | \setminus |
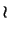 | \wr | ◊ | \diamond | 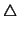 | \bigtriangleup |
 | \bigtriangledown | 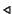 | \triangleleft | 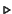 | \triangleright |
| ⊕ | \oplus | ⊕ | \bigoplus | 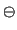 | \ominus |
| ⊗ | \otimes | ⊗ | \bigotimes | ∅ | \oslash |
 | \odot | 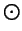 | \bigodot | 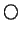 | \bigcirc |
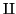 | \amalg | ≤ | \leq | 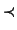 | \prec |
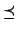 | \preceq | << | \ll | ⊂ | \subset |
| ⊆ | \subseteq | 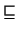 | \sqsubseteq | ∈ | \in |
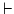 | \vdash | ≥ | \geq | 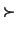 | \succ |
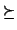 | \succeq | >> | \gg | ⊃ | \supset |
| ⊇ | \supseteq |  | \sqsupseteq | ∋ | \ni |
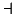 | \dashv | ≡ | \equiv | ∼ | \sim |
| ≅ | \simeq | 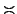 | \asymp | ≈ | \approx |
| ≅ | \cong | ≠ | \neq | 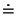 | \doteq |
| ∝ | \propto | 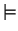 | \models | ⊥ | \perp |
| | | \mid | || | \parallel | 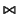 | \bowtie |
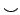 | \smile | 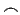 | \frown | ℵ | \aleph |
| ħ | \hbar | ι | \imath | j | \jmath |
| l | \ell | ℘ | \wp | ℜ | \Re |
| ℑ | \Im | ′ | \prime | 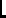 | \empty |
| ∇ | \nabla | √ | \surd | T | \top |
| ⊥ | \bot | || | \| | ∠ | \angle |
| ∀ | \forall | ∃ | \exists | ¬ | \neg |
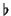 | \flat | 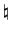 | \natural | 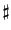 | \sharp |
| \ | \backslash | ∂ | \partial | ∞ | \infty |
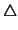 | \triangle | ∑ | \sum | ∏ | \prod |
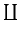 | \coprod | ∫ | \int | (∫) | \oint |
1.2.3 Arrows
| ← | \leftarrow | ⇐ | \Leftarrow | → | \rightarrow |
| ⇒ | \Rightarrow | ↔ | \leftrightarrow | ⇔ | \Leftrightarrow |
| → | \mapsto | 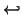 | \hookleftarrow | 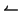 | \leftharpoonup |
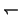 | \leftharpoondown | 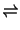 | \rightleftharpoons | ← | \longleftarrow |
| ⇐ | \Longleftarrow | → | \longrightarrow | ⇒ | \Longrightarrow |
| ↔ | \longleftrightarrow | ⇔ | \Longleftrightarrow | → | \longmapsto |
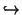 | \hookrightarrow | 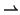 | \rightharpoonup | 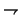 | \rightharpoondown |
| ↑ | \uparrow | ⇑ | \Uparrow | ↓ | \downarrow |
| ⇓ | \Downarrow | 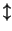 | \updownarrow | 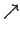 | \nearrow |
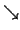 | \searrow | 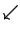 | \swarrow | 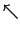 | \nwarrow |
1.2.4 Calligraphic
These characters are available if you use the \mathcal control sequence.
${\mathcal A B C D E F G H I J K L M N O P Q R S T U V W X Y Z}$
gives
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Also useful are "blackboard" style characters. \mathbb{ R Q Z}
gives R Q Z (requires the amsfonts package).
1.2.5 Character Modifiers
| \hat{e} | 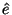 | \widehat{easy} | 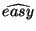 |
| \tilde{e} | 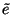 | \widetilde{easy} | 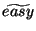 |
| \check{e} | 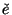 | \breve{e} | 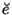 |
| \acute{e} | é | \grave{e} | è |
| \bar{e} | 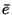 | \vec{e} | 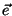 |
| \dot{e} | 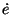 | \ddot{e} | 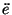 |
| \not e | 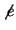 |
Note that the wide versions of hat and tilde cannot produce very wide alternatives. The `\not' operator hasn't properly cut the following letter. The Fine Tuning section on page pageref describes how to adjust this. If you want to place one character above another, you can use \stackrel, which prints its first argument in small type immediately above the second
$ a \stackrel{def}{=} b + c $
gives
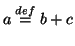 See the Macros section for how to stack characters using atop.
See the Macros section for how to stack characters using atop.
1.2.6 Common functions
In a maths environment, LATEX assumes that variables will have single-character names. Function names require special treatment. The advantage of using the following control sequences for common functions is that the text will not be put in math italic and subscripts/superscripts will be made into limits where appropriate.| \arccos | \arcsin | \arctan | \arg | \cos | \cosh | \cot |
| \coth | \csc | \deg | \det | \dim | \exp | \gcd |
| \hom | \inf | \ker | \lg | \lim | \liminf | \ln |
| \log | \max | \min | \Pr | sec | \sin | \sinh |
| \sup | \tan | \tanh |
1.3 Subscripts and superscripts
These are introduced by the `^' and `_' characters. Depending on the base character and the current style, the sub- or superscripts may go to the right of or directly above/below the main character. With letters it goes to the right.$F_2^3$produces `F23'. Note that the sub- and superscripts aren't in line. To make them so, you can add an invisible character after the `F'. $F{}_2^3$ produces F23. With ∑ the default behaviour is different in display and text styles.
$\sum_{i=0}^2 $
produces ∑i=02 (text style) but
\[\sum_{i=0}^2 \]
produces (in display style)
|
$\sum\limits_{i=0}^2$
produces ∑i=02
1.4 Overlining, underlining and bold characters
$\underline{one} \overline{two}$
produces one―two. This is not a
useful facility if it's used more than once on a line. The lines are
produced so that they don't quite overlap the text; lines over or
under different words won't in general be at the same height.
To be able to reproduce bold maths, it's best to use the bm
package. $E = \bm{mc^2}$ produces E = mc2.
Alternatively, you can use \mathbf{} to create bold characters -
$\mathbf{F}_2^3$ produces F23.
or you can use the
following idea
\usepackage{amsbsy} % This loads amstext too
\begin{document}
$\omega + \boldsymbol{\omega}$
% Use the following if whole expressions need to be in bold
{\boldmath $\omega $}
\end{document}
1.5 Roots and Fractions
$\sqrt{4} + \sqrt[3]{x + y}$
gives √4 + 3√{x + y}.
Three constructions for putting expressions above others are
- frac:-
-
$\frac{1}{(x + 3)}$ produces
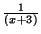 .
. - choose:-
-
${n + 1 \choose 3}$ produces
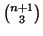 .
. - atop:-
-
${x \atop y}$ produces
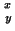 .
.
\[ \sum_{-1\le i \le 1 \atop 0 < j < \infty} f(i,j)\]
gives
|
1.6 Delimiters
| these | are made by these | and these | are made by these |
| ( | ( | ) | ) |
| [ | [ | ] | ] |
| { | \{ | } | \} |
| ⎣ | \lfloor | ⎦ | \rfloor |
| ⎡ | \lceil | ⎤ | \rceil |
| 〈 | \langle | 〉 | \rangle |
| / | / | \ | \backslash |
| | | | | || | \| |
| ↑ | \uparrow | ⇑ | \Uparrow |
| ↓ | \downarrow | ⇓ | \Downarrow |
 | \updownarrow | 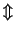 | \Updownarrow |
| (for left delimiters) | (for right delimiters) | magnification |
| \bigl | \bigr | a bit bigger, but won't overlap lines |
| \Bigl | \Bigr | 150% times big |
| \biggl | \biggr | 200% times big |
| \Biggl | \Biggr | 250% times big |
$\Biggl\{2\Bigl(x(3+y)\Bigr)\Biggr\}$
gives 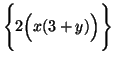 . If you're not using the default
text size these commands might not work correctly. In that case try the
exscale package.
It's preferable to let LATEX choose the delimiter size for you by using
\left and \right. These will produce delimiters just
big enough for the formulae inbetween.
. If you're not using the default
text size these commands might not work correctly. In that case try the
exscale package.
It's preferable to let LATEX choose the delimiter size for you by using
\left and \right. These will produce delimiters just
big enough for the formulae inbetween.
$\left( \frac{(x+iy)}{\{\int x\}} \right)$
gives 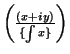 The left and right delimiters needn't be the same type. It's sometimes
useful to make one of them invisible
The left and right delimiters needn't be the same type. It's sometimes
useful to make one of them invisible
\[ z = \left\{
\begin{array}{ll}
1 & (x>0)\\
0 & (x<0)
\end{array}
\right.
\]
produces
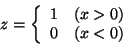 Over- and underbracing works too.
Over- and underbracing works too.
$\overbrace{\alpha \ldots \omega}^{\mbox{greek}}
\underbrace{a \ldots z}_{\mbox{english}}$
produces 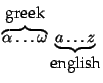
1.7 Numbering and labelling
Numbering happening automatically when you display equations. If you don't want an equation numbered, use \nonumber beside the equation. Equation numbers appear to the right of the maths by default. To make them appear on the left use the leqno class option (i.e., use \documentclass[leqno,....]{....}). Use \label{} to label an equation (or figure, section etc) in order to reference from elsewhere.
\begin{equation}
W_{\bf S}(t,\omega) = \int\limits_{-\infty}^{\infty} {
{\cal R}_{\bf S}(t,\tau) e^{-j\omega\tau} \,d \tau }
\label{LABELLING}
\end{equation}
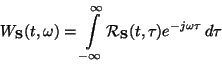 Now the following text
Now the following text
refers back to equation \ref{LABELLING}
refers back to equation 3 by number, and
refers back to the equation on page \pageref{LABELLING}
refers back to the equation on page pageref.
A file will have to be LATEX'ed twice before the references,
both forwards and backwards, will be correctly produced.
1.8 Matrices
The array environment is like LATEX's tabular environment except that each element is in math mode. The number and alignment of columns is controlled by the arguments - use l, c or r to represent each column with either left, center or right alignment. The default font style used is \textstyle but you can override this by changing the \displaystyle.
\begin{math}
\begin{array}{clrr} %
a+b+c & uv & x-y & 27 \\
x+y & w & +z & 363
\end{array}
\end{math}
produces
|
|
|
| ||||
|
|
|
|
\begin{array}{clrr}[t]
would produce top-aligned lines, and `[b]' would produce
bottom-aligned ones. The Delimiters section of this document
shows how to bracket matrices.
TEX has a few maths facilities not mentioned in the LATEX book.
The following TEX construction might be useful.
\begin{math}
\bordermatrix{&a_1&a_2&...&a_n\cr
b_1 & 1.2 & 3.3 & 5.1 & 2.8 \cr
c_1 & 4.7 & 7.8 & 2.4 & 1.9 \cr
... & ... & ... & ... & ... \cr
z_1 & 8.0 & 9.9 & 0.9 & 9.99 \cr}
\end{math}

1.9 Macros
These aid readability, save on repetitive typing and offer ways of producing stylistic variations on standard LATEX formats.
\def\bydefn{\stackrel{def}{=}}
\def\convf{\hbox{\space \raise-2mm\hbox{$\textstyle
\bigotimes \atop \scriptstyle \omega$} \space}}
produce =def and [( ⊗) || ( ω)]_endtextstyle when $\bydefn$ and $\convf$
are typed.
1.10 Packages
The following packages may be of help - (easy block matrices), (easy equations), (easy matrices), (easy tables), (easy vectors), (nested arrays), (gives more choice in theorem layout), subeqnarray (Renumbering of sub-arrays in math-mode), subeqn (Different numbering sub-arrays).1.11 Fine tuning
It's generally a good idea to keep punctuation outside math mode; LATEX's normal handling of spacing around punctuation is suspended during maths. Sometimes you might want to adjust the spacing in a formula (e.g., you might want to add space before dx). Use these symbols :-| a\, b | (a b) thin space |
| a\> b | (a b) medium space |
| a\; b | (a b) thick space |
| a\! b | (a b) negative thin space |
y & = & a + b \nonumber \\ & & + kto give
|
y & = & a + b \nonumber \\
& & \mbox{} + k
gives
|
\begin{eqnarray}
\lefteqn{x+ iy=}\\
& & a + b + c + d + e + f + g + h + i + j + k +\nonumber\\
& & l + m \nonumber
\end{eqnarray}
| |||||||||||||||||||||||
$A \over B$ \rule[-.3cm]{0cm}{1cm}{and}
1.12 Maths and Postscript fonts
It's easy to use a postscript font (like helvetica) for the text of a LATEX document. What's harder is using the same font for maths - the font will lack many of the special characters required for maths. An easy, reasonable option is to use the mathptmx package to put the maths into the postscript Times and symbol fonts where possible. Alternatively, use- the mathpazo package (loads Palatino as the text font family and a mixture of the Pazo and CM fonts for math).
- the mathpple package (loads Palatino as the text font family and a mixture of artificially obliqued Euler fonts and CM fonts for math).
1.13 Matlab and LaTeX
has some support for LaTeX production. For example
latex('(sin(x)+2*x+3*x^2)/(5*x+6*x^2)','math.tex')
puts the LaTeX representation of the expression into a file called
math.tex. Type "help latex" inside
matlab for details.
1.14 Examples
-
\begin{eqnarray} {\cal M}^2(\hat{\theta},\theta) &=& E[(\hat{\theta} - \theta)^2] \nonumber \\ {\cal M}^2(\hat{\theta},\theta) &=& {\rm var}^2(\hat{\theta}) + {\cal B}^2(\hat{\theta}). \end{eqnarray}givesM2( ^θ,θ) = E[( ^θ− θ)2] M2( ^θ,θ) = var2( ^θ) + B2( ^θ). (7) -
\begin{equation} \hat{W}_{s}(t,\omega;\phi) \bydefn \int\limits_{-\infty}^{\infty} {\hat{\cal R}_s(t,\tau;\psi) e^{-j\omega \tau} \, d \tau } \end{equation}gives^W
s(t,ω;ϕ) def
=
∞
⌠
⌡
−∞^ℜ
s(t,τ;ψ)e−jωτ d τ (8) -
\begin{eqnarray} {\cal B}(t,\omega) & \approx & {1 \over 4\pi} {\cal D}_t^2 W_{\bf S}(t, \omega) {{{\scriptstyle \infty} \atop {\displaystyle \int \! \int \! }}\atop {\scriptstyle -\infty}} t_1^2 \phi(t_1,\omega_1) \, dt_1 d\omega_1 \nonumber \\ && + {1 \over 4\pi} {\cal D}_\omega^2 W_{\bf S}(t, \omega) {{{\scriptstyle \infty} \atop {\displaystyle \int \! \int \! }}\atop {\scriptstyle -\infty}} \omega_1^2 \phi(t_1,\omega_1) \, dt_1 \, d\omega_1. \label{F4} \end{eqnarray}givesB(t,ω) ≈ 1 4πDt2 WS(t, ω) ∞
⌠
⌡⌠
⌡
−∞t12ϕ(t1,ω1) dt1 dω1 + 1 4πDω2 WS(t, ω) ∞
⌠
⌡⌠
⌡
−∞ω12ϕ(t1,ω1) dt1 dω1. (9) -
\newsavebox{\DERIVBOXZLM} \savebox{\DERIVBOXZLM}[2.5em]{$\Longrightarrow\hspace{-1.5em} \raisebox{.2ex}{*} \hspace{-.7em}\raisebox{-.8ex}{\scriptsize lm}\hspace{.7em}$} \newcommand{\Deriveszlm}{\usebox{\DERIVBOXZLM}} \Deriveszlmgives ⇒*lm
2 Graphics
Graphics can be produced- from within LaTeX - pictures can be drawn in a picture environment, but you'll find graph paper handy (xfig can create code for the picture environment). The pstricks packages is far more powerful.
- by any program that can produce Postscript files (for LaTeX) or JPEG, PNG andPDF (for pdflatex).
Whatever graphics you want to add, you should use the figure environment so that LATEX can cope sensibly with situations where, for example, you attempt to insert near the bottom of a page a graphic that's half a page high. The figure environment will float the graphic to the top or bottom of the page, or on the next page, or here (where you asked for it).
| h | here |
| t | top of page |
| b | bottom of page |
| p | on a page with no text |
The order you put these letters in doesn't matter, but whether you include them does. Putting ! as the first argument in the square brackets will encourage LATEX to do what you say, even if the result's sub-optimal. Below is a simple (and usually sufficient) usage. See the online hints for further details.
\begin{figure}[htbp]
\vspace{0.5in}
\caption{0.5 inch of space}
\end{figure}
It's possible to have more than one graphic in a figure. See the example later on.
pdflatex supports JPEG, PNG andPDF images - but not postscript. latex supports Postscript files as long as they have a proper bounding box comment; i.e. LATEX requires full
2.0.1 psfrag: adding maths to postscript files
Many packages that produce postscript output don't provide good maths facilities. It's often easier to add the maths in later using the psfrag package. This lets you replace text in a postscript file (produced with xfig, matlab, etc) by a fragment of LATEX. For example, doing
\usepackage{psfrag}
...
\begin{figure}
\psfrag{MATHS}{$x^2$}
\includegraphics{foo.eps}
\end{figure}
would display the file with MATHS replaced by x2. See the psfrag documentation for details.
2.1 Scaling, rotation, clipping, wrap-around and shadows
The graphicx package includes routines that are useful even
without graphics. \reflectbox{Reflect} produces
and \resizebox{3cm}{0.2cm}{Stretched}
produces 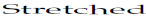 .
To scale imported graphics, use some optional arguments
.
To scale imported graphics, use some optional arguments
\includegraphics[width=5cm,height=10cm]{yourfile.jpg}
would rescale the postscript so that it was 5cm wide and 10cm high. To make the picture 5cm wide and scale the height in proportion use
\includegraphics[width=5cm]{yourfile.png}
To rotate anticlockwise by the specified number of degrees, use
\includegraphics[angle=150]{yourfile.pdf}
These options can be combined - note that order matters. The following examples demonstrate how to combine these features and how to use the subfig package to have more than one graphic in a figure.

\centering
\begin{figure}[hbtp]
\includegraphics[height=40mm]{tiger.jpg}
\includegraphics[angle=120, height=20mm]{tiger.jpg}
\caption{Tigers}
\end{figure}
% remember to do \usepackage{subfig} at the top of the document!
\begin{figure}[hbtp]
\centering
\subfloat[Small]% \quad on the next line adds spacing
{\includegraphics[height=30mm]{tiger.jpg}}\quad
\subfloat[Medium]
{\includegraphics[width=40mm]{tiger.pd}}\quad
\subfloat[Large]
{\includegraphics[height=50mm]{tiger.jpg}}
\caption{3 crests}
\end{figure}
To clip images use the viewpoint argument. The following fragment would display only part of the image. The viewport coordinates are in the same units as the bounding box.
\begin{figure}[htbp]
\includegraphics[viewport=200 400 400 600,width=5cm,clip]%
{tiger.jpg}
\end{figure}
% Use the floatflt package
\begin{floatingfigure}[l]{4cm}
\includegraphics[width=2cm]{tiger.jpg}
\caption{Using floatingfigure}
\end{floatingfigure}
Figure 4: Using floatingfigure
|
The package lets you insert a graphic and have the text wrap around it. You can provide 2 arguments to the floatingfigure command: the first (l or r) selects whether you want the graphic to be on the left or right of the page. The 2nd argument gives the width of the graphic. Not all text will flow perfectly around (for example, verbatim text fails, as illustrated below) so check the final output carefully.
Using the fancybox package gives you access to
\shadowbox, \ovalbox, \Ovalbox and
\doublebox commands, which can be used with text or
with graphics. For example, \shadowbox{shadow package} produces
 and
and
\ovalbox{\includegraphics[height=10mm]{crest.jpg}}
produces  .
Unfortunately, the fancybox package as supplied suppresses the
table of contents. The locally produced contentsfancybox solves
this, but may introduce graphics problems.
.
Unfortunately, the fancybox package as supplied suppresses the
table of contents. The locally produced contentsfancybox solves
this, but may introduce graphics problems.
File translated from TEX by TTH, version 4.03.
On 11 May 2012, 11:47.